STA 250 -- Lecture 01

Welcome to STA 250!

On the menu for today...

1. Course logistics

2. About (me|you)

3. Appetizers

• Register for a free account on GitHub
• Download the GitHub GUI at http://mac.github.com or http://windows.github.com.
  For Linux, just use the command line.
• Sign up for Piazza: https://piazza.com/ucdavis/fall2013/sta250
• Obtain an account for Gauss, the Stat Dept cluster, if you do not already have one
  • Email help@cse.ucdavis.edu to request an account.
    You must state that you are enrolled in STA 250 and email them your ssh public key.
    For instructions on how to create a public/private keypair see:
    http://wiki.cse.ucdavis.edu/support:general:security:ssh#setup.
• Email Prof. Baines your GitHub username
• Sign up as a note-taker for the course (sheet should be coming around...)

From the syllabus:

The course is designed to equip students with the basic skills required to tackle challenging problems at the forefront of modern statistical applications. For statistics PhD students, there are many rich research topics in these areas. For masters students, and PhD students from other fields, the course is intended to cultivate practical skills that are required of the modern statistician/data scientst, and can be used in your own field of research or future career.

The course is intended to be practical in nature. You will hopefully learn skills that will be useful outside of the course (be it in your own research or future work).

The modern (statistician|data scientist|person who analyzes data) needs to possess many different skills. This course also requires many different skills. You will do tasks requiring some knowledge of statistical theory, programming skills, data analysis skills, as well as some intuition and problem-solving skills.

• Efficient Bayesian computation

  • Developing fast algorithms for fitting complex Bayesian models
  • Developing efficient parametrizations/models for scalability

• Statistical applciations in astrostatistics

  • Log(N)-Log(S): Modeling astrophysical populations
  • Color-Magnitude Diagrams: Understanding Star Formation
  • Exoplanets: Using Kepler to find "Earth-like" planets

• Statistical computing using GPUs

  • Designing "GPU-ifiable" algorithms for statistics
  • Programming GPUs using RCUDA

Other random stuff: I'm English, I love dogs, I love coffee, I run, I code.

Thanks for completing the pre-course survey (those who did :)

Now for some of the results...

• Which department are you based in?

foo <- table(pcs[, 2])
data.frame(Field = names(foo), Number = as.numeric(foo))

##                                                             Field Number
## 1                                             Applied Mathematics      1
## 2                                           Biomedical Department      1
## 3                                          Biomedical Engineering      1
## 4                                                   Biostatistics      6
## 5                                                Computer Science      2
## 6                                                       Economics      1
## 7                                                     Mathematics      1
## 8  PhD student in Population Biology and MS student in Statistics      1
## 9                                               Political science      1
## 10                                                     Statistics     24

• Which degree are you enrolled in?

table(pcs[, 3])

## 
## Masters     PhD 
##       8      31

• Which of the following courses have you taken?

count_responses(pcs[, 4], cats = courses)

##    STA 108   STA 131A  STA 131BC    STA 135    STA 137 STA 231ABC 
##         31         31         27         19         19         18 
##    STA 106    STA 141    STA 243    STA 145    STA 242 
##         17         16          7          4          4

• Which of the following statistical topics are you familiar with?

count_responses(pcs[, 5], cats = topics)

## Maximum Likelihood Estimation           Logistic Regression 
##                            37                            24 
##          Mixed Effects Models                 The Bootstrap 
##                            23                            23 
##              The EM Algorithm                          MCMC 
##                            20                            18 
##          Time Series Analysis            Bayesian Inference 
##                            18                            14 
##                Random Forests 
##                            12

• Which OS's are you familiar with?

count_responses(pcs[, 6], cats = c("Linux", "Windows", "Mac OS X"))

##  Windows    Linux Mac OS X 
##       37       18       10

• What is your level of familiarity with R?

table(pcs[, 7])

## 
##                 I am an R guru! :)           I am comfortable using R 
##                                  4                                 25 
##         I have never used R before I have used R before, but not much 
##                                  3                                  7

• What is your level of familiarity with Python?

table(pcs[, 8])

## 
##           I am comfortable using Python 
##                                       5 
##         I have never used Python before 
##                                      24 
## I have used Python before, but not much 
##                                      10

• Which of the following tools/systems have you used before?

count_responses(pcs[, 9], cats = compies)

##                           Latex                       Databases 
##                              31                              12 
##                             Git                          GitHub 
##                              10                               9 
##                           Gauss Amazon Cloud Computing Services 
##                               5                               5 
##                          Hadoop 
##                               0

• Which of the following languages have you coded in?

count_responses(pcs[, 10], cats = langies, fixed = TRUE)

##          C        C++       Java        SQL Javascript    Fortran 
##         30         22         17         12          7          3 
##       CUDA      Julia     OpenCL      Scala 
##          2          2          1          1

• What fields are you most interested in applying statistical methods to?

foo <- table(pcs[, 11])
data.frame(Topic = names(foo), Votes = as.numeric(foo))

##                                                        Topic Votes
## 1                                                  Astronomy     2
## 2                                                   big data     1
## 3                                           Biological data      1
## 4                                                  Economics     1
## 5                                           Finance/Business    11
## 6                                                   Genetics     7
## 7                                        Insurance, Medicine     1
## 8                                                    Medical     1
## 9                                            Most Everything     1
## 10             neuroimaging & Multiscale data & network data     1
## 11      not really sure yet, but none of the above stand out     1
## 12                                         signal processing     1
## 13 Social Media (e.g., Analyzing Twitter, Facebook activity)     7
## 14                      Social science/media / neuroscience      1
## 15                              Sports and Physical Sciences     1
## 16                                   Stochastic Optimization     1

• Why are you taking the course?

count_responses(pcs[, 12], cats = respies)

##                                    The course sounded really interesting/useful 
##                                                                              36 
##             I am hoping that the course content will be helpful for my research 
##                                                                              27 
## I am hoping that the course content will be helpful for my future job prospects 
##                                                                              23 
##                I needed more units and it seemed like the best available course 
##                                                                               8 
##                I have to take the course to satisfy a requirement for my degree 
##                                                                               7 
##                                           My advisor told me to take the course 
##                                                                               7

• Coffee or tea?

table(pcs$Coffee.or.tea.)

## 
##            Both  Coffee Neither     Tea 
##       1      13       6       2      17

• Cats or dogs?

table(pcs$Cats.or.dogs.)

## 
##            Both    Cats    Dogs Neither 
##       1       6      11      11      10

xtabs(~Cats.or.dogs. + Coffee.or.tea., data = pcs)

##              Coffee.or.tea.
## Cats.or.dogs.   Both Coffee Neither Tea
##               1    0      0       0   0
##       Both    0    2      0       0   4
##       Cats    0    1      2       0   8
##       Dogs    0    6      3       1   1
##       Neither 0    4      1       1   4

In modern applications of statistical analysis it is common to need to model and understand highly complex processes.

Many complex processes can be decomposed into smaller, simpler, and more comprehensible pieces When combined: many simple relationships can form exceptionally complex systems

Bayesian modeling is ideal for such situations:

• It allows for "modular" (i.e., conditional) model-building
• It allows for domain scientists to introduce important "prior" knowledge
• It possesses mature computational tools to solve complex modeling problems

Lets see an example...

In many astrophysics problems it is of interest to understand the star formation process, or the age of astrophysical objects.

• What data do we have?
• How can we estimate the age of a star using that data?

There are three main properties of a star that determine its brightness:

1. Mass (denoted by \(M\))
2. Age (What we care about, denoted by \(A\))
3. Metallicity (characterized as the proportion of non-hydrogen/helium matter, denoted by \(Z\))

What we observe is the brightness of the star at different wavelengths.

A detector will typically record the brightness of the star as passed through three filters (e.g., UBV). So we have a measurement of the brightness of the star in U-, B- and V-bands.

How can we get from \((M,A,Z)\) to \((U,B,V)\)?

Fortunately, there are physical models that determine, given the mass, age and metallicity of a star, the expected brightness in each photometric band.

i.e., we have a function \(f:\mathbb{R}^{3}\mapsto\mathbb{R}^{3}\) such that:

\[ f(M,A,Z) = E[(U,B,V)] \]

In short, for each of \(n\) stars, we have noisy observations in the \((U,B,V)\)-space, and need to infer things about the \((M,A,Z)\) space:

\[ (U_i,B_i,V_i) | (M_i,A_i,Z_i) \sim f(M_i,A_i,Z_i) + \epsilon_i \]

for \(i=1,\ldots,n\). Unfortunately \(f\) has no closed form and is not invertible.

What does \(f\) look like? For fixed \(Z\), varying \((M,A)\) in the \((B-V,V)\) space we get:

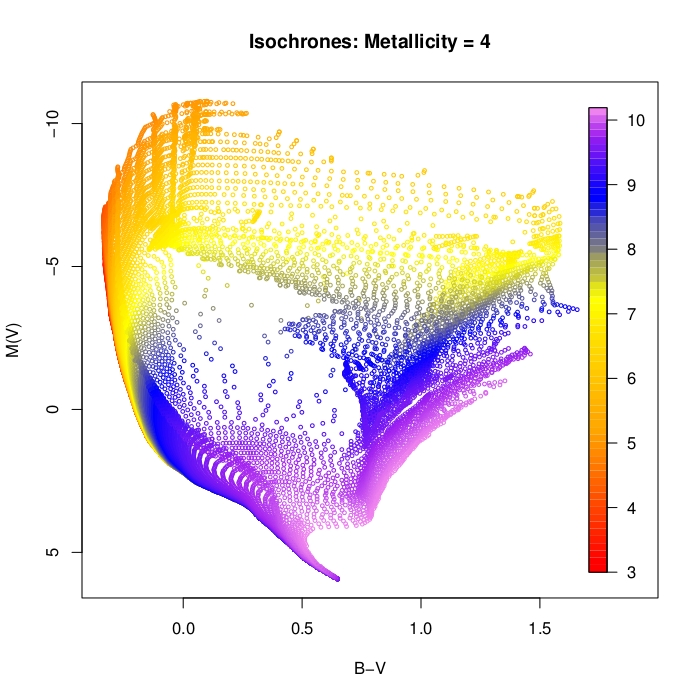
In short: the mapping is highly degenerate.

Lots of different \((M,A,Z)\) combinations give the same value of \((B,V,I)\).

Are we doomed? Should we give up and go home?

What could rescue us...?

Fortunately we have two things in our favour:

1. Prior information: We often know from previous surveys or background knowledge roughly how old, or how massive, or what range of metallicities to expect for a given dataset.

2. Pooling of Information: Stars in a "cluster" are expected to be formed at a similar time, so we can pool information across stars.

Both things can be easily done by a Bayesian model...

Observations + Science:

\[ (U_i,B_i,V_i) | (M_i,A_i,Z_i) \sim f(M_i,A_i,Z_i) + \epsilon_i \]

Pooling: \[ A_i \sim N(\mu_a,\sigma_a^2) \]

Prior Information that specifies how old, and how much variability we would expect in the stellar ages:

\[ p(\mu_a,\sigma_a^2) \]

(Other model components for \((M_i,Z_i)\) etc. omitted for simplicity).

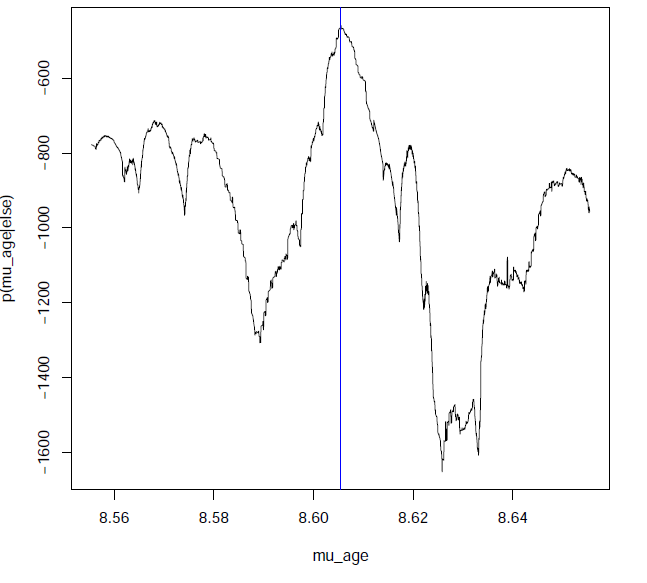
Solution: Fancy computational (MCMC) strategies.

For the 47-Tuc dataset (~1600 stars):

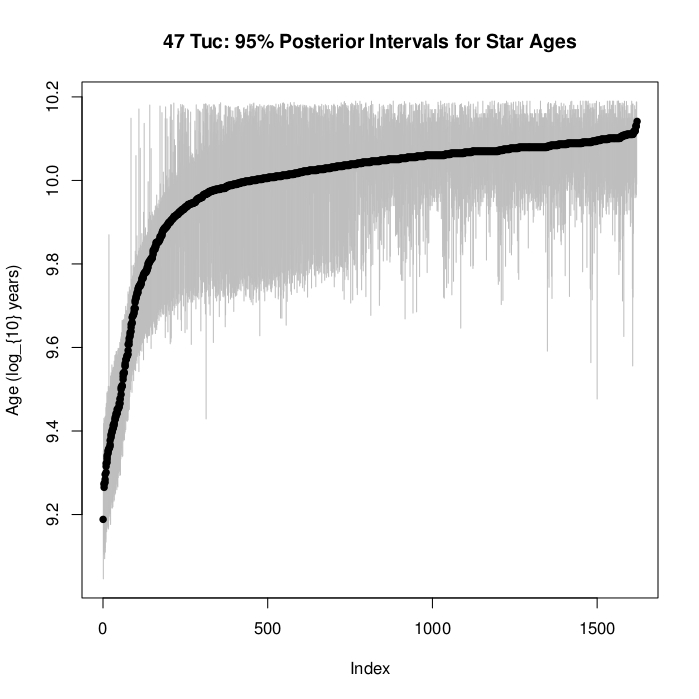
As illustrated by the astrophyics case study, Bayesian statistics:

• Can be used to provide rigorous statistical solutions to complex problems
• Allows the introduction of external scientific knowledge about a problem
• Can be used to pool information across observations in a natural manner
• Can overcome computational challenges using innovative computation

Therefore: Module # 1. :)

What is "big" data?

• Megabytes?
• Gigabytes?
• Terabytes?
• Petabytes?

• Exabytes?

• It depends what you are trying to do with it!

When dealing with data on the order of Gigabytes (or more) it becomes infeasible to read it into R and proceed as we all did back in the good old days.

How then do we deal with it?

• Clever computational tricks
• New computational infrastructure
• What statistical approaches work at such large scales?

Twitter averages 500 million tweets per day.

• That is a huge amount of data about "people": how they think, how they interact, social patterns, economic trends etc.

• Most of those tweets are lolcatz or complaints about too much foam in a cappuccino, but still, there is interesting information to be gleaned.

• Twitter has an open API that allows developers to stream samples of tweets. It is essentially possible to obtain as much data you want (and it is easy to get it).

The other day, at around midnight PT (3am ET) I streamed a small sample of about 40Mb of tweets.

Lets do the now traditional "sentiment analysis".

• "Sentiment analysis" is a branch of natural language processing that studies how to assign a "sentiment score" to a piece of text.
• The simplest procedure is very simple, but lets go with that for illustrative purposes.

• Create a "dictionary" of words, and assign each word a "sentiment score". For example:

  happy = 5 sad = -5 apathetic = -2 neutral = 0

• Go through a tweet word-by-word, and add up the sentiment scores (or you could do a per-word average)

• Words not in the dictionary are scored as zero (or omitted)

• Also, lets record the geo-tagged location (if available) of each tweet

• Lets see what we find...

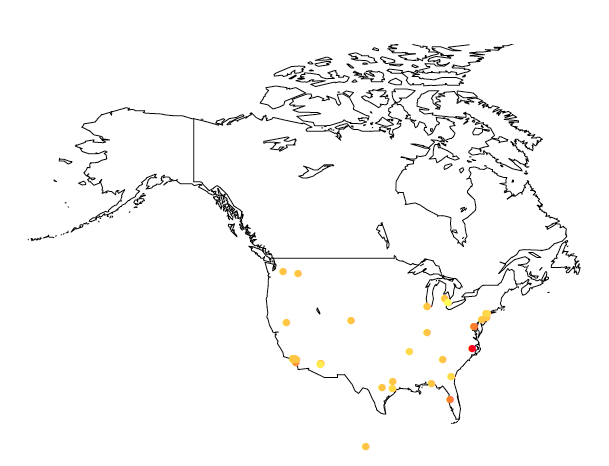
Crude, but any thoughts? Discuss.

• When datasets become truly huge, it becomes infeasible to store them on a single machine, and a fundamentally new approach to computing is needed (ensuring fault tolerance etc.).

• That is where Hadoop comes in.

• Originally developed at Yahoo!, Hadoop is a distributed file system (DFS) that can handle internet-scale datasets.

• How to interact/program with Hadoop?

• New programming models were developed, notably the Map-Reduce framework. Higher-level interfaces have now matured and are gaining popularity e.g., Hive and Pig.

• We will dive in and play with this in Module #2.

For the "big data" module (and possibly for the final project), we will also dabble with cloud computing using the EC2 and ElasticMapReduce (EMR) components of AWS. EMR provides a Hadoop environment that takes care of much of the grunt-work necessary to use Hadoop+MapReduce.

A big thank you to Amazon for providing us with an educational grant to cover course expenses! :)

http://aws.amazon.com/grants/

Any self-respecting statistician needs to know how to optimize a function.

We do this all the time, whether it be for estimation or prediction.

Knowing how to use optim is a great start, but it won't get you everywhere you need to go.

Really understanding optimization strategies can help you solve complex problems that others may struggle with.

In module 3: Optimization + The EM Algorithm, we take a look at look at optimization strategies, and an in-depth look at a very popular and useful one: The Expectation-Maximization Algorithm.

WARNING/NOTE: This will be the math-iest of the modules. ;)

Considering:

• The complexity of modern statistical models applied to cutting-edge applications
• The massive amounts of data available for statistical applications

The strain on the computing capability of statistical procedures is immense. In this module we will look at some strategies to speed up statistical computation using parallelization.

One-slide brutal simplification/history of GPUs:

Traditionally, most calculations performed by computers were done by the Central Processing Unit (CPU). CPUs can perform sequential calculations tremendously fast.

Caclucations required for computer graphics typically involve "massively parallel computation". For example, they run the same calculation independently for all pixels to produce an image. With the advent of graphics-heavy comuter games, specialist graphics cards (GPUs) were developed to conduct these graphics-related computations.

Now the cool part... since GPUs are capable of running millions of calculations simultaneously, there was much interest from scientists and non-gamers in exploiting this computing power. With the development of languages such as CUDA and OpenCL it is now possible for scientists (and statisitcians) to use the power of GPUs to accelerate scientific computation.

Thanks to:

• NVIDIA
• Duncan Temple Lang

We have access to some extremely high-powered GPUs for the course.

In module 4, you will learn the basics of GPU programming and get to play with these beasts. :)

http://cheezburger.com/7797230080

Wed: Boot camp begins!