STA 250: Lecture 8

Welcome to STA 250!

On the menu for today...

1. Types "big" data

2. Approaches to "big" data

3. Basic things about working with "big" data

4. Example: Big Logistic Regression

5. The Bag of Little Bootstraps

6. Obtaining SE's for a 6m x 5k logistic regression

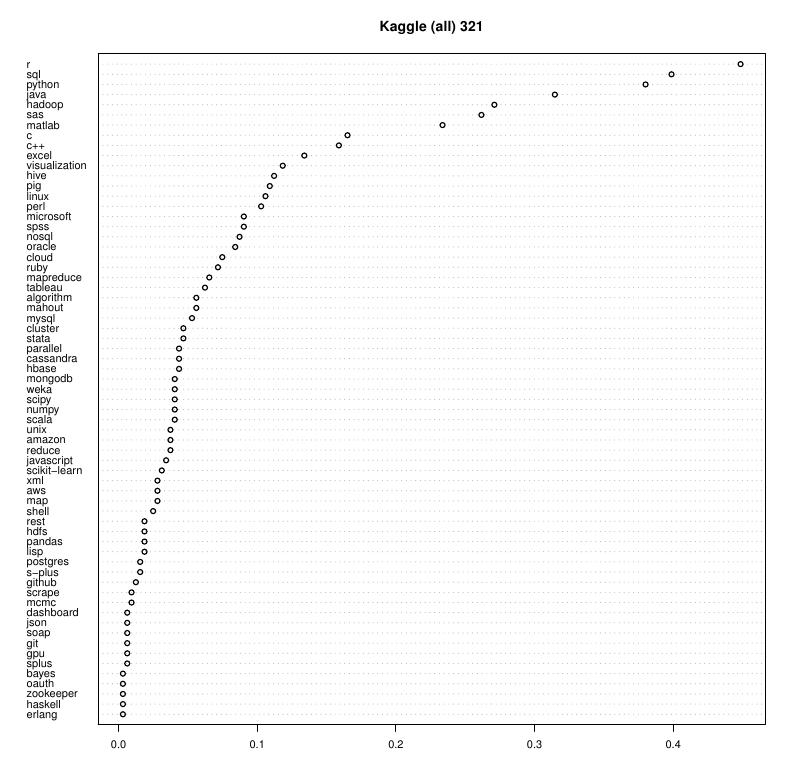
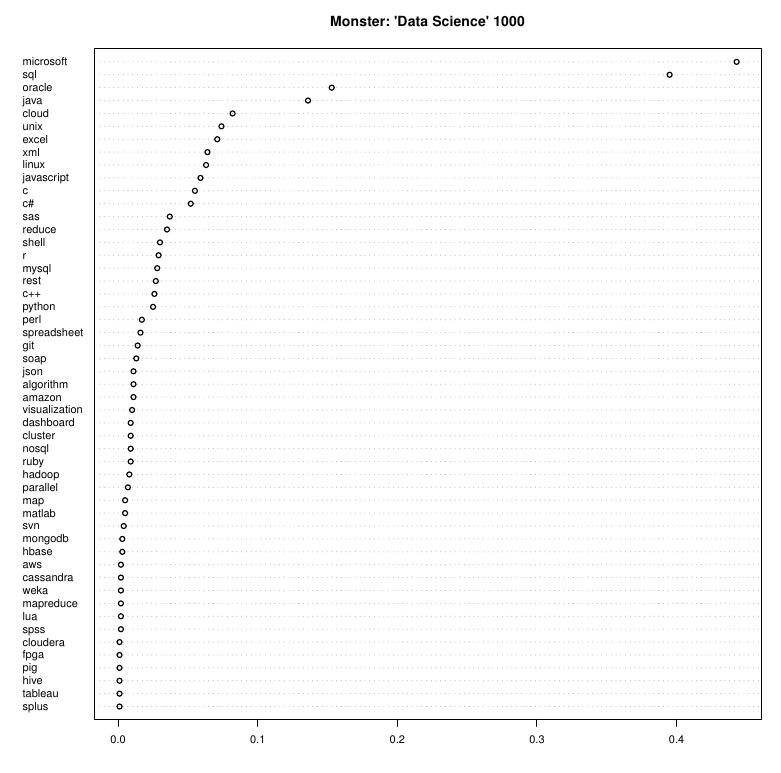
What is "big" data?

• Megabytes?
• Gigabytes?
• Terabytes?
• Petabytes?

• Exabytes?

• It depends what you are trying to do with it!

1. Large \(n\) and not large \(p\):

   • Examples I: Linear regression with 100m observations, 5000 covariates. Classification of 100m objects with 1000 features each.
   • Examples II: Website with large numbers of users, recording basic data on each user. Sky surveys in astronomy (e.g., LSST): observing millions of objects with moderate amounts of data per object.

2. Large \(p\) and not large \(n\):

   • Examples I: Linear regression with 10k observations, 500k covariates. Classification of 10k objects with 500k features each.
   • Examples II: Website with moderate number of users, tracking every action of each user. Boutique healthcare provider collecting huge amounts of data on each patient.

3. Large p and large p:
• Examples I: Linear regression with 100m observations, 50m covariates. Clustering of 10m observations with 1m features each.
• Examples II: Website with large number of users, recording large number of actions per user (e.g., Google, Facebook, Yahoo etc.). Potentially large healthcare providers (e.g., Kaiser) with large numbers of clients, and large amounts of information per client.
4. Complex (non-rectangular) "big" data:
• Examples: Financial transactions (irregular), images, movies (e.g., brain scans), Wikipedia.

Since this module is only 4 lectures, we will deal exclusively with problems of type 1.

The computational skills you will learn are equally applciable to working with the other classes of problems.

Naive approaches designed for traditional amounts of data do not tyically scale to "big" data. How to scale to big data then? Usually some combination of:

• Assuming that the data has inherently lower-dimensional structure

  • Sparsity
  • Conditional independence
    

• Fast algorithms

  • Parallelization
  • Typically linear time algorithms or better

• Methodology that avoids the need to fit the "full" data

  • Consensus Monte Carlo
  • Bag of Little Bootstraps

From the R documentation:

There are limitations on the types of data that R handles well. Since all data being manipulated by R are resident in memory, and several copies of the data can be created during execution of a function, R is not well suited to extremely large data sets. Data objects that are more than a (few) hundred megabytes in size can cause R to run out of memory, particularly on a 32-bit operating system.

We can't read in data to memory, so what alternatives are there?

1. File-backed data structures (i.e., data remains stored on disk, not memory)

   • Examples: bigmemory (and other big* packages). See: http://www.bigmemory.org/
     
   • Pros: Easy to use. Simple to understand, any language can mimic functionality.
   • Cons: Requires "nice" data, burden on programmer to scale algorithms (parallelization etc.), doesn't scale as easily to data that cannot fit on disk.

2. Databases

   • Relational Databases (e.g., SQL): Rigid structure, relational algebra operations (union, intersection, difference etc.).
     
   • NoSQL Databases (e.g., CouchDB, MongoDB): Less structure than a relational database, less functionality, but typically faster data retrieval.

3. Distributed File Systems
• Example: Hadoop Distributed File System (HDFS). Data remains on disk, but DFS provides a full ecosystem for scaling to data across multiple machines.
• Pros: Scales to essentially arbitrarily large amounts of data (just add more machines).
• Cons: Harder to interact with data. More restrictive progamming paradigm (MapReduce).

In this module we will work with (1) and (3), as well as learning a little bit about databases.

Lets start with a practical example using method (1).

On Gauss I have created an uncompressed 255Gb file containing data for fitting a "big" logistic regression model (6m observations, 3k covariates).

Goal: Find standard errors for the parameter estimates of the logistic regression model.

To do this:

1. Figure out how to work with that much data using bigmemory (or Python equivalent)
2. Figure out how to obtain standard errors for parameter estimates in a scalable manner.

(Could just as well ask for CI's in place of SE's)

The basics:

# Create a file-backed big.matrix:
# (Takes ~minutes, and creates large .bin file, and small .desc file)
goo <- read.big.matrix(infile, type="double", header=FALSE,
                      backingpath=datapath,
                      backingfile=backingfilename,
                      descriptorfile=descriptorfilename)

# Attach that big.matrix:
dat <- attach.big.matrix(dget(descriptorfile),backingpath=datapath)

This is actually overkill for what we will need here (and quite inefficient), but in some cases the extra functionality is useful.

For example, to fit "big regressions" with biglm.big.matrix or bigglm.big.matrix.

Can still do the basics (they just might take a while!):

# First row:
dat[1,]
# Number of rows:
nrow(dat)
# First two rows, first ten columns:
dat[1:2,1:10]
# Random sample of 5 rows:
dat[sample(1:nrow(dat),5),]

We actually won't use any of the real functionality of the bigmemory suite of packages. All we really need is the ability to read arbitrary lines from a file without loading the full file into memory.

• load the file
• Read line-by-line until the desired line is reached

• Extract the data from the line

  def read_some_lines(filename,lines):
      # output lines specified by lines e.g., [1,100,10000]
  

  
  "read_some_lines" = function(filename,lines,max_block=1000,verbose=FALSE){
      # output lines specified by lines e.g., c(1,100,10000)
   }
  

Now we have the data in: that is progress.

We are fitting:

\[ Y_{i} | \beta \sim \textrm{Bin}\left(1,\frac{\exp\left\{x_{i}^{T}\beta\right\}}{1+\exp\left\{x_{i}^{T}\beta\right\}}\right) , \quad i=1,\ldots,6000000 . \]

Goal:

• Find elementwise CI's or SE's for \(\hat{\beta}\).

How might you do this for small datasets?

We talked about the bootstrap during boot camp.

Suppose we have an estimator \(\hat{\theta}=g(X)\) (e.g., the MLE).

The basic Bootstrap algorithm (Efron, 1979) to approximate \(SD(\hat{\theta})\) is:

1. Let \(\hat{F}\) denote the empirical probability distribution of the data (i.e., placing mass \(1/n\) at each of the \(n\) data points)
2. Take a random sample of size \(n\) from \(\hat{F}\) (with replacement).
   We call this a "bootstrap dataset", and denote them as \(X^{*}_{j}\) for \(j=1,\ldots,s\).
3. For each of the \(s\) bootstrap datasets, compute the estimate \(\hat{\beta}^{*}_{j}\).
4. Use the standard deviation of \(\left\{\hat{\beta}^{*}_{1},\ldots,\hat{\beta}^{*}_{s}\right\}\) to approximate \(SE(\hat{\beta})\).

With independent observations this works well. There are more sophisticated modifications for dependent data (e.g., spatial data, time series data etc.).

For the logistic regression model, we have both \(X's\) and \(y's\).

When we resample points, we resample both \(x_{i}\) and \(y_{i}\). This is sometimes called the paired bootstrap.

There are other alternative bootstrapping procedures (e.g., bootstrapping the residuals) with possibly better/worse performance.

For the logistic regression problem, using \(B=500\):

1. Let \(\hat{F}\) denote the empirical probability distribution of the data (i.e., placing mass \(1/6000000\) at each of the \(6000000\) data points)
2. Take a random sample of size \(6000000\) from \(\hat{F}\) (with replacement). Call this a "bootstrap dataset", \(X^{*}_{j}\) for \(j=1,\ldots,500\).
3. For each of the \(500\) bootstrap datasets, compute the estimate \(\hat{\beta}^{*}_{j}\).
4. Use the standard deviation of \(\left\{\hat{\beta}^{*}_{1},\ldots,\hat{\beta}^{*}_{500}\right\}\) to approximate \(SD(\hat{\beta})\).

Any problems here?

Now, lets introduce the "Bag of Little Bootstraps" method (Kleiner et al., 2011).

The basic idea:

• Would like bootstrap datasets to be small enough to fit!
• Just using bootstrap datasets with \(b < n\) won't work without rescaling
• Instead: sample \(s\) subsets of size \(b < n\) and then resample \(n\) points from those.
• No rescaling necessary!
• Key 1: There are only (at most) \(b\) unique data points within each bootstrapped dataset (each occuring possibly many times).
• Key 2: We can scale to very large \(n\) if \(b << n\) and the estimation routine works efficiently with data of the form (unique datapoints, number of occurences)

For estimating \(SD(\hat{\theta})\):

1. Let \(\hat{F}\) denote the empirical probability distribution of the data
   (i.e., placing mass \(1/n\) at each of the \(n\) data points)

2. Select \(s\) subsets of size \(b\) from the full data (i.e., randomly sample a set of \(b\) indices \(\mathcal{I}_{j}=\left\{i_{1},\ldots,i_{b}\right\}\) from \(\left\{1,2,\ldots,n\right\}\) without replacement, and repeat \(s\) times).

3. For each of the $s$ subsets ($j=1,\ldots,s$):
• Repeat the following steps $r$ times ($k=1,\ldots,r$):
1. Resample a bootstrap dataset $X^{*}_{j,k}$ of size $n$ from subset $j$.
   i.e., sample $(n_{1},\ldots,n_{b})\sim{}\textrm{Multinomial}\left(n,(1/b,\ldots,1/b)\right)$, where $(n_{1},\ldots,n_{b})$ denotes the number of times each data point of the subset occurs in the bootstrapped dataset.
2. Compute and store the estimator $\hat{\theta}_{j,k}$
• Compute the bootstrap SE of $\hat{\theta}$ based on the $r$ bootstrap datasets for subset $j$ i.e., compute:
$$ \xi^{*}_{j}=\textrm{SD}\left\{\hat{\theta}^{*}_{j,1},\ldots,\hat{\theta}^{*}_{j,r}\right\} . $$
4. Average the $s$ bootstrap SE's, $\xi^{*}_{1},\ldots,\xi^{*}_{s}$ to obtain an estimate of $SD(\hat{\theta})$ i.e.,
$$ \hat{SD}(\hat{\theta}) = \frac{1}{s}\sum_{j=1}^{s}\xi^{*}_{j} . $$

• How to select \(s\)? (Number of subsets)
• How to select \(b\)? (Size of subsets)
• How to select \(r\)? (Number of bootstrap replicates per subset)

Real key is \(b\). From paper \(b\approx{}n^{0.6}\) or \(b\approx{}n^{0.7}\) works well.

What is the gain then?

• Why does the BLB algorithm work?

• How can use the array job capabilities of Gauss to help speed things up?

• How might you organize the array job in terms of the subsets and bootstrap replicates?

• What can you do if each data point occurs multiple times?

Today we have seen how to obtain SE estimates for potentially huge datasets using very minimal advanced computing. In fact, it only took two key steps:

• Avoid reading data in memory using bigmatrix

• Avoid fitting full dataset using the BLB

Next week we will look at more general computing tools and paradigms: MapReduce, Hadoop, Hive, and using Amazon ElasticMapReduce.

http://icanhas.cheezburger.com/ Mon: More big data!